The Biggest Smallest PNG
A few days ago, my former coworker Evan Hahn posted “The world’s smallest PNG”, an article walking through the minimum required elements of the PNG image format. He gave away the answer in the very first line:
The smallest PNG file is 67 bytes. It’s a single black pixel.
However (spoilers!) he later points out that there are several valid 67-byte PNGs, such as a 1x1 all-white image, or an 8x1 all-black image, or a 1x1 gray image. All of these exploit the fact that you can’t have less than one byte of pixel data, so you might as well use all eight bits of it. Clever!
However again…are we really limited to one byte of pixel data?
(At this point you should go read Evan’s article before continuing with mine.)
When “Compression” Isn’t
The shortest uncompressed image data chunk contents for a PNG is two bytes: one byte to introduce the current “scanline” (row) of pixels, and one byte for the pixel data (which can be up to 8 pixels if you’re encoding a black-and-white PNG). Evan represents this as 00 00, since he’s encoding a single black pixel with no filter. But then there’s a “compression” step, and even ignoring the additional attached header and checksum those two bytes turn into a 4-byte “DEFLATE” block: 63 60 00 00.
What a worthless compression algorithm, right? Well, not really. It is mathematically impossible for every input to a (lossless) compression algorithm to get shorter, for the same reason that it’s impossible to assign every letter of the alphabet a unique number between 1 and 10: no matter how hard you try when going the other way, you’re only going to produce ten possible outputs. This is the pigeonhole principle, and it’s not really a problem in practice: most of the time the things you want to compress aren’t random or extremely short, and so there’s room for improvement. We’re just in a weird edge case where that’s not true.
Anyway, Evan mostly skipped over DEFLATE (which, totally fair, there’s plenty to say about PNG), but left in a footnote about what was in those four bytes:
The first bit signifies that this is the final DEFLATE block. The next 2 say that this is block that uses hard-coded Huffman codes; no “dictionary” is included in the payload. The next 8 bits encode a literal zero, and then another 8 bits encode the same. The next 7 bits are the “end of block” marker, and the final 6 pad the data so that it’s byte-aligned.
He also recommended the infgen tool for playing with DEFLATE, which gives the same breakdown:
% infgen -dd evan-deflate-block
! infgen 3.2 output
!
last ! 1
fixed ! 01
literal 0 ! 00001100
literal 0 ! 00001100
end ! 0000000
! 000000
At which point I stopped to ask myself: is that really the best we can do?
A self-referential format
The LZ77 compression strategy that DEFLATE uses saves space by encoding “backreferences” to earlier parts of the string, rather than wastefully repeating those bytes. (Many years ago Julia Evans did an extremely neat visualization of how these backreferences work by using poetry, which I highly recommend taking a look at to get some intuition for how this works.) One somewhat surprising property is that these backreferences can overlap with themselves; the explainer Evan found for DEFLATE uses the string “Blah blah blah blah blah!” as an example, which compresses to “Blah b[distance=5, length=18]!”1 (I’m not going to explain that here, click through to the DEFLATE explainer to see how it works.) Can we use that to our advantage?
From the breakdown above, we know the block is going to be a minimum of 18 bits: the last flag (1 bit) + the compression scheme fixed (2 bits) + at least one literal 0 (8 bits) + the end marker (7 bits). If we could squeeze out a second byte of output in 6 bits, we’d beat Evan’s record (because our DEFLATE block would only be three total bytes long), but unfortunately there’s no way to do that in DEFLATE. So instead, we assume we’re going to match Evan’s 32 bits total, and we have to decide how to use those remaining 14 bits. Evan’s straightforward encoding used 8 bits to encode the second 00 byte, and left 6 bits as padding. What alternatives do we have?
I scanned through RFC 1951, the DEFLATE spec, and found this in section 3.2.6, “Compression with fixed Huffman codes (BTYPE=01)”:
Lit Value Bits Codes
--------- ---- -----
0 - 143 8 00110000 through
10111111
144 - 255 9 110010000 through
111111111
256 - 279 7 0000000 through
0010111
280 - 287 8 11000000 through
11000111
(Note that these “codes” are written backwards from how infgen displays them. The “endianness” problem gets even worse when you start talking about bits grouped into bytes instead of just bytes grouped into multi-byte integers.)
To summarize a second table, values 0 - 255 are literal bytes (like the “literal 0” above), 256 is the end marker, and 257 - 285 are “length codes” for backreferences. (286 and 287 are unused.) Which means we’re in business! We can encode an overlapping backreference rather than a second “literal 0”, and repeat that first 00 N times.
The way backreferences are encoded is a bit tricky, and I’m not going to go into it here; if you’re curious you can poke through the tables in the RFC like I did. Fortunately, the longest possible backreference has a relatively simple encoding: #285, i.e. 11000101, followed by a fixed 5-bit “distance” encoding of 00000 (i.e. “zero bytes back from the most recent byte”). Putting this together gives us a DEFLATE block of 63 18 05 00, or
% infgen -dd jordan-deflate-block
! infgen 3.2 output
!
last ! 1
fixed ! 01
literal 0 ! 00001100
match 258 1 ! 00000 10100011
end ! 0000000
! 0
This decompresses to a series of 259 zeros, still encoded in just 32 bits. (31 bits, even.)
What can you do with 259 zeros?
As Evan points out, you have to spend one byte to introduce a new row in a PNG. If we’re trying to maximize the number of pixels in our 67-byte PNG, we should therefore put them all in one row, so we only have to pay this cost once. That results in 258 bytes of pixel data, which at 1 bit per pixel gives us a whopping 2064 pixels.
Which, after updating all the CRC32 and DEFLATE (Adler-32) checksums, produces this PNG. Which I’m not even going to bother embedding, because there’s no good way to show a 2064x1 image on a vertically-scrolling website layout. As a consolation prize, here’s a 48x37 image (1776 pixels), which is the closest to square you can get with 259 zeros:

Evan set a lower bound on the size of a PNG file, and now I think I’ve set an upper bound on the contents of a valid2 smallest-possible PNG file. But I’d love to be wrong!
Appendix A: Do we have to use zeros?
Technically no! The byte has to be a valid “filter type”, which can be 0 “None”, 1 “Sub”, 2 “Up”, 3 “Average”, or 4 “Paeth Predictor” (sic), but then we can repeat that as pixel data as much as we want. Encoded as bits, that’s 0000_0000, 0000_0001, 0000_0010, 0000_0011, or 0000_0100. Here’s what the other four rectangles look like:

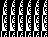


*shrug* Not much use for these but there you go!
Appendix B: Tools used in the creation of this post
As noted, I used Mark Adler’s infgen tool (the one Evan recommended) to play with and check my DEFLATE blocks. I used Python’s zlib.decompress() to check that I got the zlib checksums correct without needing to update the PNG checksums.
For calculating the PNG checksums, I used crc32. (Note that these include the header name but exclude the length field.) I did the Adler-32 checksums for zlib by hand (well, I constructed the arithmetic expressions, then let the computer evaluate them). This was a bit silly because I could have used Python’s zlib.adler32().
For hopping in and out of hex on the command line, I used xxd. xxd -r -p goes from text hex to binary, allowing spaces, which was useful for passing into crc32.
On a Mac, I recommend doing hex editing in Hex Fiend. And I didn’t do anything special to open the resulting PNGs; if they worked, they displayed in Preview just fine. I did also use pngcheck to examine what was in the file.
-
With sufficient cleverness, this can be used to construct a compression quine, a “compressed” file that produces itself when you “decompress” it. ↩︎
-
Who puts a footnote in the wrap-up paragraph? Sheesh. Anyway, in trying to test all this I constructed a handful of PNGs that declared widths or heights bigger than the number of pixels I had. Preview still opened them and
pngcheckstill declared them valid. What’s going on? My guess is that this is supposed to help with reading truncated or corrupted files—rather than rejecting them outright, it’s more useful to show the user the data that is there. I didn’t explore the precise limits of what’s accepted or rejected, though; I already spent enough time making this post! ↩︎
